Note: here is the Power BI file, the file contains the data model and all the DAX
I tend to differentiate between two categories of DAX statements
- DAX statements that calculate a numeric expression and
- DAX statements that are searching for specific members inside a column or table
Sometimes, things become a little blurry as a DAX statement may contain parts of both categories.
A simple example of calculating a numeric expression, e.g., is the calculation of the YoY Growth of Total sales. An example of a search is looking for the TOP N customers.
This article is about searching.
Quite often, I encounter tasks that are similar to the following one: Find all the customers from the US, with a Total Sales > xyz. Depending on the data model, this type of question can be answered quickly, even without using DAX.
But sometimes, questions become more tricky. Take some time and consider the following question: Find all the customers from the US, with a Total Sales > xyz, who bought red and green products together. Sometimes rigor is put to this question by adding "and only red and green products, no other colored products in addition" to the question.
Answering this kind of question using Power BI has to tackle the following underlying challenges:
- Multiple selections of values (colors) are combined by an OR and not by an AND
- Selecting only two colors means that the customers have to be identified who bought the selected colors and just the selected colors
Some theoretical background
I'm not aware of any other term or phrase used to name this specific task that is different from this one: relational division. For this reason, I will stick to this phrase, and admittedly I like the nerdy touch that comes with it. After introducing the name, it makes sense to explain what's behind the name. Relational Division is one of the basic operations of relational algebra invented by E.F. Codd ("A Relational Model of Data for Large Shared Data Banks", 1970). This operation uses one table (the divisor) to divide another table (the dividend), the result (the quotient) of this relational division, often a single column that represents a subset of the domain of the dividend, then can be used to further refine the analysis of the available data.
If you think this sounds strange or weird, you are right. But being able to name a problem very often is the first step in solving the specific problem and similar problems more easily. Nevertheless, it's time to provide an example. The data has been taken from here (http://dbazine.com/ofinterest/oi-articles/celko1/), as this is very popular regarding the relational operation – relational division.
The task is simple: Find the pilots who can fly the planes inside a hangar.
As we are using Power BI, the 1st step is to look at the data model:

A relatively simple data model, a pilot table with all the pilots, a plane table that contains all the planes, and a table called PilotPlane that lists the pilots and the planes the pilots can fly.
The role of the hangar mentioned in the task, will be played by a slicer. Then the task can be rephrased to: Find the pilots who can fly the selected planes.
To be close to the original these are the planes of interest:
- B1-Bomber
- B-52 Bomber
- F-14 Fighter
Selecting the above planes from the planes slicer will find the pilots:

Unfortunately, this is not a valid answer to the question.
A closer look at the PilotPlane table shows the following:
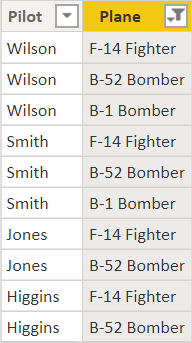
Just the pilots Wilson and Smith can fly all three selected planes. The pilots Jones and Higgins are "just" able to fly two of the selected planes.
Finding just the pilots Wilson and Smith is not as simple as we might wish. Maybe this is one of the reasons why this relational operator is not being directly implemented in SQL query dialects as other operators like INTERSECT or UNION.
Throughout all the years, I never encountered any data model with pilots, planes, and hangars, but I encountered very often questions like the following:
- Identify all the customers who bought specific products together
- Identify engineers/consultants/contractors who possess specific skills
- …
Relational division and Dax
DAX is not different from SQL in providing answers to this specific type of question. It takes a little thinking and weighing of odds (meaning considering data distribution) to create a DAX measure that helps to identify just the two pilots. But before we delve right into DAX, it's necessary to be aware of two variations of the relational division; one is called exact relational division, and the other one relational division with remainder. The exact relational division identifies just the pilots who can fly the exact number of selected planes only. In the context of the above example, this means that if the F-14 Fighter and B-52 Bomber are selected, only the pilot Jones must be identified. As all other pilots who can fly the F-14 and B-52 are also able to fly additional planes.
In contrast, the relational division with remainder returns all four pilots by selecting these two planes, here the algorithm does not care, that Higgins, Wilson, and Smith can fly more planes than the two selected.
Regarding the implementation of implementing the relational division operator DAX is not different from SQL; it requires some thinking to find the pilots Wilson and Smith (relational division with remainder) or just Smith (exact relational division).
Relational Division exact
The pbix file "Relational Division the plane example - public.pbix" contains two measures reldiv - exact and reldiv - more complex. The 1st measure implements an algorithm to identify pilots based on exact relational division and is used on the report page "exact relational division." The 2nd measure is used on the report page "more complex relational division"
This is happening inside the measure reldiv – exact:
- A table variable is created that contains the selected planes, the number of the selected planes is stored to another variable.
- A table variable is created that contains pilots used as the starting point for the ultimate search. Here a virtual table is created that contains the pilots who can fly at least one of the selected planes.
-
- SUMMARIZE(…)
-
- Returns a table that contains all the pilots that can fly (at least) one of the selected planes.
- ADDCOLUMN(…)
-
- The column "@abc", contains the number of planes a pilot can fly from the selected planes. This is achieved by leveraging the DAX function COUNTX. As the …X indicates, COUNTX is one of the table iterator functions. Each time the numeric expression returns a value that does not equal NULL or zero, the value is counted. From my point of view, COUNTX is somewhat underused as it can be used to count how often a numeric expression returns a value. A question that can be answered by using COUNTX is: Find all the customers whose Total Sales exceeded y, for each of the last 12 months. The table to be iterated contains the last 12 months, the numeric expression (a measure) returns a value if Total Sales is exceeding y. COUNTX has to return 12, to identify a customer that satisfies the condition. Here COUNTX is also used to overcome the conditional OR that is used to filter the PilotPlane table.
- FILTER(…)
-
- is used to filter the virtual pilots table to only the pilots that can fly the number of selected planes only.
Relational division - the self-service approach
The second measure honors the combination of multiple selected items, meaning the combination of selected items using OR (the Power BI default), but also allows searching for an exact match and a match wit remainder.
This measure "reldiv – more complex" is used on the 2nd report page "more complex relational division".
As there are three types of search, there is a manual table that lets the user decide what search type will be used. These are the possible search types:
- At least one (the Power BI default)
- At least the selected (relational division with remainder)
- Exact (exact relational division)
The measure uses a similar approach as the measure "reldiv - exact" but for more flexibility, a table iterator of the filtered pilots is used.
The numeric expression used with the iterator is more complex, as it recognizes the selected searchtype.
Have fun searching
Kommentar schreiben